Ra-Hoor-Khuit Network's
Other Thelemic Authors
Other Thelemic Authors
David George Mattichak Junior
(If you want to reach David and comment on any of his
works email him directly)
The key to the order & value of the English Alphabet as foretold in the Book of the Law
To Begin; I am David Mattichak, I am 37 years old and I live in Melbourne Australia. I am not associated with any organizations, sects, orders or anything else of that nature. Even though I am making such a grand claim, I have no interest whatever in pursuing the mantle of a Prophet or a messiah in any form, neither do I think myself to be the re-incarnation of Aliester Crowley, Jesus Christ nor anyone else of any note. I am, in short, an ordinary fellow with an ordinary life who has had an extraordinary experience, an epiphany if you will.
I have been a student of the occult, or magick, for twenty years, but in that time I have never joined any official groups, and the only real formal training in the Art which I have received came from a Priest of Wicca, who instructed me in the method of making the magick circle and other such elementary processes. He also assisted me through my first initiation (which a perusal of my Magick Diary of the time shows contained an Elevenfold Invocation to ABRAHADABRA, even though I had at that time no knowledge of Thelema or of the true nature of this Key Word. It was included because of the Alexandrian influence of the Wicca group which initiated me), which was of course Wiccan in nature. Shortly thereafter my teacher died and I was left to be instructed by a Witch who was to some extent my teachers direct heir. This turn of events culminated in my abandoning Wicca altogether (or almost so, anyway), as I was really interested in Magick not religion. I decided to take up the method delineated in The Golden Dawn, and to adhere to traditional methods of practice as much as possible, the upshot being that I began a Probationary Period on 8 April 1982 (on this Day Sol being in Aries, and Luna in Libra, all of the outer Planets exhibited a retrograde motion in the heavens). During this time I devoted myself entirely to the study of Magick and nothing else. I worked my way through the Golden Dawn material, systematically and thoroughly. Though I still retained my link to my Witch friend, and her assistance was invaluable, I worked during this period almost entirely on my own. It was during this period that the companions who had begun the Path with me began to fall by the wayside.
My involvement with The Book of the Law began on 27 of January 1983, when one of the aforementioned companions loaned me a copy of The Book. I read the MS, and returned the copy vowing to get it for myself, but that was the end of it and my diary for the period makes no further mention of it until September. So it was that on these days that I went against the direct commandment of Ankh-af-na-Khonsu and I studied & discussed the Book, before returning it instead of shunning my friend and destroying the Book after my first reading as I should have. Indeed his words have been prophetic and I have paid the most dire & perilous price for this, my Folly. At the termination of this Year and a day, I formally Self Initiated again, basing my ceremony upon the Golden Dawn Neophyte Ritual. I followed this with the Ceremonies for the Elemental Grades as I came to them so that by September I had essentially exhausted this volume, save for the Adeptus information. At the end of my self imposed period of probation to magick, my material resources having been completely depleted, I returned to the work force, and until September my studies were very sparse. During August though my employment came to completion and I was again free to take up my studies.
Since my first look at The Book of the Law, my friend who owned the particular copy and I had rented lodgings together and so I had access to his library. It was for this reason that on Sept 1st 1983 I again studied the exact same volume of The Book of the Law, and saw in it a straightforward Invocation to the Goddess Nuit, which I immediately determined to employ. Performed that night, as directed by the Book, the immediate result was that the Temple filled with a deep purple light which had about it the quality of a mist, yet totally without any substance. The effect of this on myself was that I was dazed and awestruck by the experience, seeing very clearly the nature of myself and my motivations in the world. Also, I began to see more very straightforward orisons in the text to invoke the other Gods mentioned in the Book. Upon the afternoon of Monday the 5th of September at 15:00 I saw upon Page 16 of the Third Chapter of the Book of The Law, drawn as a line and a circle squared, the Key to the Order & Value of the English Alphabet.
On this day I was at my leisure, and consequently I had the time to peruse the Book again, though I was beginning to feel as if I had about exhausted it as a resource to my Great Work. How mistaken can one be? From The Confessions of Aliester Crowley I had learned that the key of the Book had been discovered by Frater Achad, and I had accepted that the mystery was solved. On that Monday afternoon I couldnt believe what I was experiencing, when like a lightning bolt, the whole key was communicated to me from the page of this most venerable & terrible Book. This Holy Talisman had awakened the seed within myself, which I now know to have been planted there long before my birth. The experience was as if the world were filled entirely with Light, but that I was so dazzled that I was unable to perceive it. My ears filled with a sound like a rushing torrent and my heart beat as if it would burst. Yet in the midst of this I felt the greatest calm that I have ever known, before or since. My instant reaction wasnt what have I found here?, rather I was instantaneously aware of the meaning and potential, and also the certainty of my epiphany. Seventeen years of study has just continued to confirm this last.
The key which I have found has all of the qualities required of the key as it is described in the Book. The nature of the key describes the order, value and symbols attributed to the English alphabet, simply and without the need for any prior knowledge save for some simple mathematics and the contents of the series of letters called the Alphabet. Each of the points of reference upon Page 16 of the Third Chapter of the Book are met, the line, the circle squared in its failure, And Abrahadabra, as are the references in the 55th verse of the Second Chapter. My studies then turned to the obscure passage at Chapter II vs. 76, with its string of alpha-numeric characters. This verse opened up, as I shall demonstrate later in this note, to reveal a ritual or ceremonial format for attaining the Sacred Magick, and for achieving Abrahadabra, Union with the Goddess.
This formula then suggested three ceremonies, one for Nuit, Hadit and Horus (Ra Hoor Khuit/Hoor Paar Kraat). I set about constructing these rituals, using as much as possible the text from the Book itself for my Orison. The first ritual, performed on September 6th 1983,to Nuit, had the effect upon me of putting me into a trance which lasted for some 4 hours or more, until some people actually physically shook me out of it in the fear that I was dead. Apparently I was almost not breathing and I had gone entirely rigid so that I was able to be lifted and moved about quite easily. I have no recollection of these events though, as my memory is of only a passing moment of perfect bliss. These events were witnessed by at least six people, none of whom are in the least bit inclined to Magick or Thelema.
The second ceremony, performed September 8th 1983, to Hadit, had the effect of making me awake (this is the best description I can give). For the next 48 hours I did not sleep, eat or stop for rest in any way. During this time I constructed the Third ceremony which I had postulated, the one to Horus. The ceremony to Hadits results had begun to worry my companions, my girlfriend at the time left because she was determined that I was set out to kill myself by these magicks. I personally was reveling in my accelerated pace of consciousness, caught up in the moment and unable to perceive beyond it. In this frame of mind then, on September 10th 1983, I performed the third postulated ceremony drawn from the alpha-numeric string in ChII vs.76, invoking Horus as Ra Hoor Khuit-Hoor Paar Kraat. The immediate result of this ceremony was that a voice, yet without sound, instructed me to sit towards the West, facing Westward in my asana, which I did, and in the smoke of the incense which I had placed there, there appeared a veil or a curtain. The smoke of the incense had fanned out into this same shape, and as this occurred, the veil parted and a Holy Symbol, not unlike One mentioned in The Book of the Law, appeared to me from beyond this curtain. This Image moved into the Magick Circle from the West, and appeared as if it were pure radiance. The Image remained with me in the Magick Circle for several minutes, during which time I was aware of receiving some sort of charge or energy. When this process appeared complete, the Image retreated exactly as it had appeared, save in reverse, and the veil closed. After this the temple was filled with a white radiance, bright enough to read by, even though the candles and lamps which lit my orison had long since extinguished themselves.
This was by far and away the most dramatic result of any ceremony which I had ever performed. I had had a certain amount of success at evocation, and certainly I could make a Talisman flash, as described in the Golden Dawn papers, but this was beyond the scope of even what I had imagined magick to be. To this day, I still cannot believe the result of this ceremony, and my own implied involvement in the Book of the Law. I had never set out to find any key, and to the dedicated Hedonist that I am, the burden of responsibility which this thrusts upon me is certainly not desirable. Finding this key to the Gematria of the English Alphabet never fit in with my original plan in life in any way whatever. I have never, and still do not, have any aspirations to be a spiritual leader, master, messiah, beast, child of therion or any other thing than I am, but if my discovery is truly the key mentioned in The Book of the Law, then I am in fact connected to the Book and certain of its prophecies relate to me also. The idea that somehow my life might not be entirely my own, and motivated by some of the more dire oracles in the MS, I determined to verify or negate my discovery by whatever means it took.
Firstly I went to the writings of The Beast himself, as indicated in the First Comment, (which I had been unaware of at my reception of the Book, to my subsequent peril). This passage following appears to be a Qabalistic test (on the regular pattern) of any person who may claim to be the Magickal Heir to The Beast. Be ye well assured all that the solution, when it is found , will be unquestionable. It will be marked by the most sublime simplicity, and carry immediate conviction.. It was apparent then, that the Beast had determined that the key must be something so basic, and without the need of artifice, that it would be immediately recognisable. Further, it would consist of one, or very few elements and it would require no other prerequisite knowledge other than the basic Qaballah and Tarot familiar to the least students of the Art & Science of Magick. Without at least that basic knowledge the Key would be pointless anyway. Also I investigated as thoroughly as possible the veracity of the account of the Beast himself as to the communication of The Book of the Law.
Since the Holy Qaballah of the Hebrew language relates so closely to the Key, I determined to use it as a Yardstick by which to measure the veracity of the values of the letters given by my key. Thus I defined the parameters of acceptable manipulation to those specified by the Beast in his Qabalistic writings. Foremost of these being Gematria, 777 & Sepher Sepheroth, although the Golden Dawn and a smattering of other texts have been referred to also, but in essence everything of my explanation of this key has been drawn directly from the Beasts works listed above. At the same time, the English Gematria & Qaballah must at least begin to stand on its own as a coherent system of spiritual expression.
I also determined that the Key must be the simplest answer conceivable to the problem, following the advice of William of Occam that ENTITIES ARE NOT TO BE MULTIPLIED WITHOUT NECESSITY. The key must also fit to all passages soever in the MS, and elucidate something of the meaning held therein, even if only to confirm what is written in plain English. Therefore the parameters of the inquiry must (I) be in consonance with the spirit of The Book of the Law (II) be correspondent to traditional ideas of Qaballah, at least superficially (III) adhere to the principals of Common Sense &(IV) satisfy all of the internal proofs indicated in the MS. Armed with these yardsticks I now set out to determine the field of the inquiry.
A short perusal of a Chart of the Heavens for Cairo on April 8th, 9th & 10th 1904, reveals Sol to be in Aries of course, the Sign of Tzaddai mentioned in the first Chapter, but not notable really. The conjunction of Mercury & Mars on the cusp of Aries & Taurus is notable though, lending weight to the Beasts account of a communication from Harpocrates, but Crowley was no doubt aware of this peculiar heavenly arrangement, so it is perhaps contrived. The movement of Luna over the Three Days brings Her into conjunction with Saturn, and the Ascendant on all three occasions is occurs on the cusp of Cancer & Leo. Most notable though is that at the specified time all nine Planets (even the undiscovered Pluto) were above the Horizon, save Uranus, Mercurys greater Brother. These few correspondences, whilst not proof of anything, are very suggestive, lending weight to Crowleys story. From his account of the event in The Confessions of Aliester Crowley and in The New Comment on Liber Legis though, I am convinced that he is at least telling most of the truth. I have had twenty years to consider the mans work and I have ended up coming to the conclusion that he had his version of every story, and he was sticking to it, but I feel that in the matter of The Book of the Law he was totally sincere, perhaps only because discretion is the better part of valor, either way the truthfulness of the MS is certain in my mind.
Chapter II Pages 14-15 vs. 55 Thou shalt obtain the order+value of the English Alphabet; thou shalt find new symbols to attribute them unto. Which seems to define the Key as I have discerned it. The arena of the research is then (a) the Alphabet, its order and the value of it as a whole and integrally by its components & (b) new symbols to which the Alphabet may be attributed. These components then, are to be measured by the yardstick of the Holy Qaballah to test their veracity or fallibility.
Next, I considered what is meant by the English Alphabet. This inquiry eventually led to my formally studying Typography, the study of scripts esp. printed type, and of the graphic structure of letters and words. An Alphabet (from Greek Alpha-Beta or Hebrew Aleph-Beth) is :a system of letters, esp. arranged in conventional order). This begs the questions (1) What are letters? & (2) What is their conventional order? Letters (from Latin:Litera) are conventional (ie. We all agree upon their significance) mark used to express a sound in speech. Speech is composed of two types of sounds, which have English letters, Vowels and Consonants, and the letters are therefore divided into these two groups (as every third grade schoolchild knows). A Vowel is: a speech sound produced by the unimpeded passage of the breath (modified by the vocal chords) through the mouth, different Vowel sounds being made by altering the form and position of the tongue and the lips. (from the Latin Vox:voice). Consonant, meaning: consistent, suitable, harmonious, in the form of a noun means: an articulation which can be sounded only with a Vowel, a letter of the Alphabet representing such a sound (latin con:with sonare:to sound). This is important, for there must be a distinction between these classes of letters, for a various times the Vowels have been omitted in part or wholly, from the English or Latin Alphabet which we now know. This Alphabet can be best described as A System of standard marks which represent the vowel and consonant sounds of the English spoken language (ie. letters), arranged in a conventional sequence. If any of these conditions fail to be met it is no longer an Alphabet of English letters, merely a line of written gibberish.
From its name, the Alphabets origins can be deduced. Alpha-Beta or Aleph-Beth are, of course, the beginning of the sequence which contains the letters of the Greek or Hebrew Alphabets. The English letters in common use today are directly derived from the Latin Script, and that is a direct descendent of the Etruscan Script. Our first Alphabet thus appeared in the 7th Century B.C. and there was no sign for o, i or u, only A & E which related more to a soft aich sound than to Eee. This Alphabet was called by the Etruscans the Aabecedearia, indicating even then the importance of the sequence. By the 6th Century B.C. the Latin Script, known as a borrowing script for its propensity to borrow letters from other scripts, combined the Etruscan Script with a now extinct Greek Script from lower Italy, and the modern Alphabet was more or less complete. This Alphabet was then A, B, C, D, E, F, (G), H, I, K, L, M, N, O, P, Q, R,S, T, V, X. The letter I was actually abolished in 312 B.C. by Emperor Appius Caecus, and replaced with a Y. It was also common practice in Rome to omit the Vowels altogether from inscriptions, or to replace O & U with V. Our Alphabet began to stabilise into its current format around the beginning of the first millenium, and became standardised with the inclusion of all of the vowels as well as W & Z after the advent of the printing press (see Sign Symbol & Script- Hans Jensen, George Allen & Unwin 1950 trans. 1970) . The conclusion of this is that the existing order of the English Alphabet is the only one which gives it conventional definition. Further, this order will imply the Value in a sequential system of enumerating the letters, by the consequential nature of both series, letters and numbers. This too implies that the correct order will bear upon the new symbols to attribute them unto.

Page 16 of the Third Chapter of The Book clearly states what the Keys will be to the one who shall see them. The page is drawn over (or under?) with a gridwork of lines at 1 inch intervals. Along the y axis of this grid, the letters a, b, c, d, e, f, g, h of the English Alphabet are clearly marked. Likewise, along the x axis of this grid, the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 are clearly written. Drawn across this grid is a handwritten line and a figure which the text refers to as this circle squared. The text upon the page continues the verse begun upon page 15, adjuring that the Book be translated into all tongues, but to retain the original MS because therein are graphically evident properties which will facilitate the discovery of the key of it all. Indeed the Beast is told not to try for thereby alone can he fall from it. The text then delineates the conditions which will reveal the key, indicating that the time of its discovery is not the time of the writing of the MS. These indicators are three, (1) this line drawn is a key (2) this circle squared in its failure is a key also (3) And Abrahadabra. The one who shall (shall has the root meaning of an obligation or fealty) find this key shall be his child, and that strangely. Whoever finds the key will of course be obliged to follow the Beasts work, and therefore be his child figuratively speaking. The origin of this child is not stated, whence implies that the time and place of this person is not communicated, only that the three devices are his method. My epiphany involved the position of the line and the circle squared in its failure, thereby fulfilling the conditions set out above. Upon the day which I saw the solution drawn on this page my attention was attracted instantly to the graph, I assumed that this was the Key which had been found by Frater Achad, and that I was having a moment of clarity about this marvelous Book. The combination of the graphic qualities of the page and the content of the text came together in my head and I realised the equation which calculates the value of the letters. I assumed immediately that this was general knowledge because of the simple nature of the rule described.
When I was in school, I had studied pure & applied mathematics and I was thoroughly familiar with Simultaneous Equations (when I found the key I had only been out of school for 18 months). The line, which I defined as in mathematics as having no breadth or thickness, only length, only defined by two points through which it passes (ie. The distance between two places etc.). Examination of this line will show that it has only two such points clearly marked upon the grid, c=3 & d=5. This line generates the simple equation x+2=y+1. No doubt this line possesses many other concealed properties, but this one is openly apparent. The circle squared was immediately clear to me as the rule of the equation. A circle is a plane figure bounded by a single line, every point of which is equidistant from a fixed point called the centre. Squared means adjusted to a standard based upon four-sidedness. The position of the circle is then being related to the sides of the page. This circle, with a cross to mark its centre, is a definitely articulated mark which is squared in relation to the gridwork and thereby to the line drawn. The placement of this mark is in the grid denoting the value seven which should be attributed to e in the normal scheme of things, but this mark indicates that the vowel should have the same value as a, which is 0, thus the circle to mark its place as crossed out, further, having two out of five vowels thus valued implies that the series vowels is all valued at 0. So by its failure (falling short, cessation or omission etc. from Latin fallare:to deceive) and by the word also, at the end of this stanza, connecting this symbol with the line drawn, this circle squared indicates that the rule of the equation of the line is that the Alphabet has the Vowels removed from the sequence of values. This point of view is strengthened by the value of a being 1 by the calculation of the line. This being the first letter in the sequence, though makes it also a positive emanation and therefore +1, thus (-1)+(+1)=0, and a too has no numerical value. Applying this rule I found the equation : For B=1 (Alphabet-vowels)+1=(value of letter)+2. This gives the values of a=0, b=1, c=3, d=5, f=7, g=9, h=11, j=13, k=15, l=17, m=19, n=21, p=23, q=25, r=27, s=29, t=31, v=33, w=35, x=37, y=39 & z=41. I am certain of the order of the Alphabet (vide supra), and then it follows that by the equation of the line and the circle squared that these are the values.
The new symbols in Ch II vs. 55 then would fit to a schema of twenty-two letters, but which schema? New, lately made or produced, is from the Latin Novus & the Greek Neos as in Neophyte. The adjuration though is to find these symbols which implies that they already exist and then the meaning of new might be, different or additional. A symbol is defined as that which by custom or convention represents something else (from the Greek symbolon: a token, syn: together & ballein: to throw), so it would appear that these symbols are of a scale of twenty-two, already extant and of a conventional nature. If these twenty-two letters are then applied sequentially to the Paths of Sepher Yetzirah, and the Tarot Atus, then the new (ie. previously not done) symbols are the familiar ones of Qaballah, and the rest is straightforward.
So then, if these are indeed the values and symbols which the Book attributes to the English Alphabet, then the next requirement of it is to test it upon some significant word or phrase, that is to put it into action, Solvitur Ambulando! Fortunately the Book itself offers the immediate solution to this conundrum by supplying the stanza, And Abrahadabra. And by implying by these words that the Word Abrahadabra is in itself a Key. The Beast had elucidated the true form of this Word The word Abracadabra is familiar to everyone. Why should it possess such a reputation? Eliphas Levis explanations left me cold. I began to suspect that it must be a corruption of some true word of power. I investigated it by means of the Cabbala. I restored its true spelling. (The Confessions of Aliester Crowley relating to an incident which occurred in 1899 at least 4 years prior to the Book of the Law). From his studies he had already elucidated also that Abrahadabra was a perfect glyph of the Great Work accomplished, and that its Gematric value was 418, which thus made that number a fit numerical expression of the Great Work also. Indeed prior to 1904 the Beast had deciphered the entire Hebrew Qaballah of this Word (see Gematria). As such, any interpretation by an English Gematria should be in consonance with these same principals.
The poor grammar of this stanza, beginning with a conjunction, implies that both words are to be included in this Key. And is from the Germanic root ante, against, which implies that the values of the letters revealed in the previous two stanzas is to be measured against the Word Abrahadabra. The values of this phrase by the values calculated by the line & circle squared are And:26 & Abrahadabra:72. 26+72=98. Fortunately, the Beast deals with the numbers 26 and 72 in his book Gematria. 26=IHVH, Jehovah as the dyad expanded (ie. Achad=13x2), the God of Nature, fecund, cruel, beautiful, relentless. 72=Chesed, Mercy and most importantly, 72 is the number of the Divided Name, Shemhamporesh (see the Book of Lies Ch. 72). This word is that which if spoken will annihilate the created Universe. This name represents the Name of God in its entirety and it is closely connected with the 72 Quinaries of the Zodiac. Note also I+IH+IHV+IHVH=72. This number is then already connected with the completion of the Great Work and there is a certain consonance, but the connection is only rudimentary. Closer examination of the Word Abrahadabra, though reveals that it has three distinct parts, although only two forms are evident (this is suggestive in itself). The Beast himself notes this in his official Comment: AL I, 1: Had! The manifestation of Nuit! compare this with Ch II vs 1, the compliment of this verse. In Nu is Had concealed, by Had is Nu manifested. Nu being 56 and Had 9, their combination is 65, Adonai the Holy Guardian Angel. Also Hoor who combines the force of the Sun with that of Mars. Adonai is primarily Solar, but 65 is a number sacred to Mars. See the Sepher Sepheroth, and The Wake World, in Konx om Pax for further details on 65. Note moreover, the sixty-five pages of the MS of Liber Legis. Or, counting NV 56, Had 10, we get 66, which is S=1 to11. Had is further the centre of the Key-Word ABRAHADABRA. Crowley, the old Comment on Liber Legis. These two forms are ABRA and HAD.
Abra, has a value of 28 which is S=1 to 7, the mystic number of Netzach, the seventh light upon the Tree of Life, and thereby it is related to Venus, the Goddess of Love. Further, 28=14x2, 14 being the number of DVD, beloved. 28 being an extension of the Holy 7 into the Elemental Sphere combined with the other mathematical qualities which it possesses, qualify this syllable as at least being feminine, related somehow to Love and to Victory. In the Word, this syllable is repeated twice, with the syllable Had dividing the two. 28x2=56. This is the Number of Nuits Word Ch I Pg 5 I am Nuit and My Word is six and fifty. As Nu is the compliment of Had, everything about the Key word which is Not Had is Nuit, thus Nuits Word is Divided for Loves sake to conceal Her compliment Had (see quote above).
Had is sixteen, foursquare. A number possessing many qualities mathematically being 8x2, 4x4, 2 to the fourth power etc. and therefore the ultimate expansion of the Dyad already mentioned in relation to Abrahadabra above. Note also that the sixteenth Atu of the Tarot is The Blasted Tower, attributed to Mars/Horus. 16 is considered to be a number of Death (see Ch. 16 The Book of Lies). The Key Word can further be broken down into syllabic portions: AB=1 + RA=27, which is three cubed or a symbol of the trinity extended into 3 dimensions. By this, every part of Nuit is a Unity expressing itself in the material world as a trinity (but this may stretch the parameters of the investigation).
98 though, is a more complex problem as a number. Mathematically 98=49x2 or the square of 7 doubled. This represents the Holiest of Integers extended as a Word. The Holy Qaballah renders the God Name HUA ALHIM, He is Gods. The Words ChMN, hid or concealed, as well as ChSL, to consume, to eat & TzCh, White; -all very suggestive, as if the Gods had concealed their whiteness in this short stanza, laying there latently, waiting to consume men and eat them up with blindness (this last stretches the parameters of this inquiry though so it isnt put forward formally, merely included for consideration). It is noticeable that the Temurah of And Abrahadabra is 26=2+6=8 & 72=7+2=9, giving the value in a complimentary manner. Also 9+8=17 the number of IAO connecting this stanza with the expression of the Trinitarian Godhead and with the formula of Initiation by redemption. After much study of the Book by this Gematria I discovered that And Abrahadabra=98=Glad Word (Ch II vs. 76s final two words (as it also equals Come Forth, Supreme, ill-ordered, achieve Hadit and an endless number of other phrases, no doubt. This stretches the point of this investigation though.).
In Ch. III Pg 16 vs. 47 the Key is defined by the line drawn & the circle squared as: For B=1 (the letters of the Alphabet-the vowels)+1=value of the letter+2. When applied to the third Key in the verse it renders the value of 72 for the Word Abrahadabra, obviously linking it with the concept of the Divided Name Shemhamporesh, a glyph of the totality of our concept of Godhead and one of the cornerstones of the Hebrew Qaballah (that is; the number 72 indicates every Name of God). The value of And implies IHVH the formula of consecration, and so the stanza becomes an adjuration to Invoke Nuit and Hadit in their conjunction, by the Word Abrahadabra. It is also notable that 47, the number of the verse, is the value of HADIT and that the Page number 16 is the value of HAD (note also in my reproduced page 16 which is the one that suggested the solution is numbered 72, my copy being from 93 Publishing, issued Dec. 22 1975, Quebec Canada, but this is just a coincidence I am sure, I had never noticed this before scanning the original for this paper.).
To return briefly to Ch II vs. 55, the order & value have been found, will this key also indicate exactly which new symbols, to attribute them unto? Examination of this phrase reveals that new=56 and symbols=134, 56+134=190, S=1 to 19, the mystic number of Leo, Atu XI Lust, the Beasts own Tarot Card. The value of New=56 indicates Nuits symbols and this is borne out by the total correspondence to Atu XI an image of great importance to Qelhma. The Gematria of the new key then, corroborates the reasoned out solution to the problem, just as the other two conditions of this verse have also been fulfilled. Finally, the phrase attribute them unto renders the values 121, 61& 52. 121 is the square of 11 and thereby an extension of the idea of the Magick Light. 61 is AIN, the Negative, Not and unto=52, the number of AMA, the Supernal Mother, and also the value of Nuit in English, indicating in simple terms that the symbols must represent the Magick Light and the Negative Goddess. The total value of 234 indicates graphically a series and the whole passage seems to verify the choice of the Holy Qaballah and the Tarot Atus as our system of symbols. From these points a Qaballah equivalent to the Hebrew and Greek may begin to be constructed.
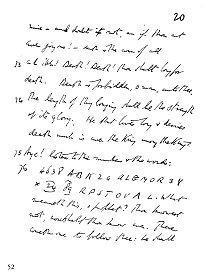 |
 |
Having fulfilled the obligations of Ch. II vs. 55 to obtain the order & value of the English Alphabet, also, having found the new symbols to attribute them unto (note that order=59-the yoni calling for the lingam as ovum see 777 & value=50 The number of the gates of Binah, whose name is Death see Gematria , thus these parameters are indicative of Nuit & Hadit, and 59+50=109 which is AiGVL:circle, sphere also very suggestive). Then, having put the new values for the letters to the test, first with the Key word, and then by a re-examination of ChII vs55, the results so far seem positive enough to at least continue the experiment. In the passage from his Comment quoted above, the Beast determines that Ch II vs.76, with its puzzling string of alpha-numeric characters is a Cabalistic test (on the ordinary pattern). This string of characters was written in eleven distinct groups (unexceptional in itself as the Beast was certainly subconsciously looking for such correspondences himself, especially in light of what he knew about Abrahadabra-vide supra). The text of the verse makes a point of phrasing a question for the Beast in two short stanzas. The answer is in two more short stanzas, and finally two more short stanzas predicting the one who will expound this mystery. The end of the verse addresses o chosen one to be me & to go into the world and tell them this Glad Word.
From the question, the answer begins to be implied, meaneth=82 the number of ChSID:righteous, holy and this=71=ALIL Nothing, and ALM:Silence. 82+71=153=(S=1 to 17) and is thus attributed to the Path of Zain and thereby to the Twin Gods. Knowest=131=SMAL the Averse One indicating the Books opposition to the Beasts possession of this Gematria. Know=71 which is a number of apparitions (vide supra and this is in agreeance with the Beasts own Comment upon this topic (see The New Comment to Liber Legis) ), ever=60 ATU XIV implying science or synthesis and 71+60=131 again tempting the Beast to look for his child.
Now the text goes on to describe that There cometh one, cometh=64 an extension of 8, being its square whilst also being 2 to the 6th power, indicating its basis in the Word, which is extended to a consciousness. 64 is also the number of DIN & DNI twin Mercurial Intelligences, implying that the coming is as a messenger. One=21 which is the mystic number of Tiphareth implying that this one is a conscious entity. 64+21=85 the full enumeration of the letter Peh, and thereby the attribution is to Mars/Horus. Follow=76=AiBD, slave or servant, indicating the office of the follower to be that of a servant to Hadit.
This one shall, ie. Is obliged to, expound that is to interpret or to explain in a certain way (from Latin: ex, out postulatare, to demand). Expound=86, the number of ALHIM and thence of the Pentagram, and the Elements. Thus the Gematria outlines that the one will purify the knowledge of the English Qaballah and explain its Elements (note that it=31the number of AL and certainly one of the relevant numbers of the text and that by the Yetzirac attribution of Atu XVI the Blasted Tower or the House of God, a card with a specific relation to the text). The value of chosen=64, so the one that cometh is identified numerically with o chosen one and the entire Gematria is identical save the yetzirac attributions, cometh has identical letters save for the m & t, Atus X & XVI, chosen replaces these with s & n, Atus XV & XI, in either case the sum of the Atus is 26 IHVH.
This chosen one is adjured to follow (vide supra) the love of Nu, look=32 which is of 64, thereby half of the purpose of the choosing, and forth=76 (vide supra) but the service now is to men. The other half of the purpose of the chosen is to tell these men this glad word. Glad=31=AL the number of God, and Word=67, the number of Binah, thus this glad word imparts the Understanding of God (there are no doubt many deeper correspondences also but the superficial and obvious are what must concern us in this experiment). 31+67=98. This is the enumeration of And Abrahadabra (vide supra) and so it immediately answers the question mark left dangling over the enumeration of the third key from ChIII Pg 16 vs.47, the Glad Word is Abrahadabra, not only the precepts of Qelhma and the text of The Book of the Law. The implication of the text, though, is that this Glad Word is the string of characters from this verse which the chosen one will expound. Thus the connection which the Beast made is further strengthened.
By attributing the groups of characters to the letters of ABRAHADABRA sequentially, the following arrangement results:-
| A:4638 B:ABK R:2 4 A:ALGMOR H:3 A:Y D:X A:24 B:89 R:RPSTOVA A:L |
Could this be some formula for invoking Abrahadabra, for uniting the Macrocosm with the Microcosm in the completion of the Magnum Opus? Perhaps the Beast even sensed something of this as he wrote the Words of the text, and he manipulated the characters into what he had hoped would appear as eleven groups, he hints as much in the New Comment to this verse. In any event the Beast was certain that this verse formed the acid test of the whole Key.
The string of characters is made up of nine numbers but eleven digits, and nineteen literal characters but only fourteen letters, these arranged into six Words. These six words are made up of three single letter Words, one three letter Word, one six letter and one seven letter Word. The numbers may be broken down to five groups, thus six literal and five numeric expressions form the structure of this string of characters, again strengthening the association with Abrahadabra.
- 4638=21=3
- 2 4=6
- 3 = 3
- 24=6
- 89=17=8
The total value of this string may be calculated variously as 21+6+3+24+89=143 which is 13x11, Achad, Unity, extended by the Magick Light or perhaps expressed as an elevenfold Word. The sum of 3+6+3+6+8=26 the number of tetragrammaton, implying that the numeric portion, at least, relates to consecration by invocation. 21 is S=1 to 6 and is the Mystic number of Sol.6= S=1 to 3, and is the Mystic number of Binah, the Supernal Mother. Likewise 3 is the mystic number of Chokmah, the Supernal Father. 24 is 72/3 and also the number of Elders in the Apocalypse (see Gematria). 89 is the number of Silence and of Restriction (see 777).
Equally, the Words, or literal characters, may be investigated by Qaballah. 19 is the number of the feminine glyph, having the same value as Eve, and the word for manifestation (see 777 & Sepher Sepheroth), thus the letters are connected to Nuit as the numbers are connected to Hadit (as IHVH the One God). The five numerical groups imply the elements and the Pentagram, whilst the six literal groups indicate the Hexagram and the Planets, whilst indicating the Sephiroth of Tiphareth at the heart of the Planets.
- ABK=0+1+15=16 (Had)
- ALGMOR=0+17+9+19+0+27=72 (Abrahadabra)
- Y=39 13x3 unity as a trinity, and YHVH Achad, God is One.
- X=37 is Yechidah, the Highest principal of the soul (see Gematria).
- RPSTOVA=27+23+29+31+0+33+0=143 11x13 (vide supra)
- L=17 IAO, the Swastika and thereby Aleph and the Word itself.
The sum of these six Words is 324, 18 squared, the number of Shekinah, the Glory of God and a number related to the Atu VII the Chariot (see The Vision and the Voice). 143+324=467, a prime number with the enumeration of Golgotha, the place of skulls from the crucifixion. By Temurah 4+6+7=17, the number of IAO and the whole then expresses that this is the Word of the Place of the Sacrifice of Initiation (see the Golden Dawn Adeptus Ritual).
All of this connects the formula in its entirety as a formula for initiation, and that to the unity of ABRAHADABRA. The numeric expression formulates Hadits portion of the formula and the literal characters express Nuits. The mystic numbers indicated are those of the Father, The Mother and the Son, the symbolism is that of Tetragrammaton, and so it represents the Work of the Wand. The values of the other numerical expressions relate to Abrahadabra as a Trinity and to Restriction & Death, thereby to Hadit, but even this Death is that of redemption for the Temurah of 89 is 17 which is IAO.
Each of the six sets of literal characters, which as a whole represent the feminine, but individually represent aspects of the Masculine Diety, in harmony with the Beast's concept that Nuit expresses Herself as Hadit. 16=HAD the point experience, 72 is Abrahadabra union with its compliment in the Dyadic expression 0=2 (see the Book of Thoth). 39 is YHVH Achad, the Unity expressed as a Trinity, 37 is the Yechidah, Hadit within Man, 143 is Unity expressed as Abrahadabra and 17 is IAO, the word itself.
In addition to their numerical value, the letters also have a new symbolic value, their Tarot attribution (the Beast himself often used this means of Qaballistic investigation see-the Magickal Diaries of Aliester Crowley etc).
- ABK: 0 Fool (Air) , I Magus (Mercury) , VIII Adjustment (Libra)
- ALGMOR: 0 Fool (Air) , IX Hermit (Virgo) , V Hierophant (Taurus), X Fortune (Jupiter) , O=0, XIV Art (Sagittarius)
- Y: XX Aeon (Fire)
- X: XIX Sun (Sol)
- RPSTOVA: XIV Art (Sagittarius), XII Hanged Man (Water), XV Devil (Capricorn), XVI Tower (Mars), O=0, IV Emperor (Aries), 0 Fool (Air)
- L: IX Hermit (Virgo)
The first group of Atus renders the total IX, or 3 squared and expresses Had (16) as the Fool and the Magician and He Who Equilibrates the Two. The next set gives the total XXXVII, which is 418/11, connecting in this Word both the Beasts own excellent extrapolation of Abrahadabra with the value given by this Key (vide supra the value of this string is 72=Abrahadabra). XX is Yod spelt in full, and expresses the Holy Guardian Angel, as well as Kaph the Palm and the open hand of God, thus the Trinity of Godhead extends its Hand as the Holy Guardian Angel. XIX is the feminine principal, this time expressed as twin children (see The Book of Thoth). The next long string of characters renders the total value of its Atus as XLVII, the number of the Yoni as dynamic & fertile, the espirit de travail (see 777 introduction) connecting the essence of this Word as being the attainment of unity by Abrahadabra (vide supra 143). 47 is also the enumeration of Hadit. Finally, the L at the end of the two lines has been written alone in the MS, and its Atu IX is 3 squared as above, but Hadit is now expressed as the Hermit, the Microcosm conscious of its own divinity. The Hermit is also a traditional token of the Holy Guardian Angel, indicating that the result of the performance of a ceremony or discipline based on this formula ends in His Holy Communication. As suggestive as these results are, the acid test mentioned above is in the interpretation of the two lines of figures as a whole.
| Thus: | A:4638 the integers imply 4/the Elemental Weapons 6/the |
| Hexagram & LVX 3/the Trinity and 8=2 cubed, will made manifest and also a number of Mercury and of analysis. B:ABK the Words of this work are an analysis of the division of the Light from the Darkness. Combining this interpretation with the material in the previous portion and the Pentagram and Hexagram Rituals are strongly suggested. R:2 4 Chokmah is Wisdom & Harmony, but also the Dyad & Division, its action upon itself is to double or to square itself (the only number to possess this property of the sum of itself with itself also equaling the product of itself by itself). Chesed is Mercy and the Form of all positive existence, being AL God and also Law, that being natural law. The Path joining Chokmah with Chesed is Vau, Atu V the Hierophant implying that the officer here is the initiator. The synthesis of Will and Form, Wisdom and Mercy which forms the essence of the Truth communicated by the Word Abrahadabra, which the Hierophant imparts. |
|
| A:ALGMOR | is the Word which brings together the Holy Guardian |
| Angel, as the Hierophant implied above, and the True Will (X Fortune) in spiritual synthesis. This Word is Abrahadabra as the basis of the Oath (Atu V the Hierophant
see Magick in Theory and Practice Ch XVI). Again the combination with the first portion is suggestive of the Oath, that which gives Will its Form is the statement of intention, which taken before ones Holy Guardian Angel becomes ones sworn obligation and in itself a symbol of the Great Work completed as the Union of subject and object, thus equating it directly with Abrahadabra, 72. H:3 is Binah and thereby the Supernal Mother, Nuit. H, the Letter of the Word related to this portion, is Atu VI The Lovers or the Brothers, and implies direct orison, ie. To the Supernal Mother. It also indicates oracles and prophecy, both attributed to Nuit. (note that the Hebrew for H is He and attributed to Aquarius, Atu XVII The Star & the Goddess, by a more direct means) A:Y Abrahadabra expressed as the Word of a Trinity, but this Trinity is apprehensible as the Word of the Initiating Hoor, the Holy Guardian Angel. Thus combining this with the portion above, the Goddess Nuit is to be Invoked by Her Word, that is Abrahadabra, this Word is to be uttered by the Adept inspired by Hoor manifest as His Holy Angel. Thus the formula of Tetragrammaton is indicated here, the last He being recalibrated by this symbolism to imply total identification. D:X The Supernal Triad apparent as Harmony, Beauty, and the exaltation of the consciousness. A:24 The Word Abrahadabra expressed as a portion of its trinitarian whole ,24=2x3x4 indicating a serial progression, this is partly why it is used as it is in Revelations. Combination with the previous portion indicates that after the Union with Godhead has been accomplished that the portions of that unified consciousness are re-identified and then one is selected for attention, suggestive of the progression of the conjuration by the formula of Tetragrammaton (see Magick in Theory and Practice Ch II & III). B:89 this is the number of DMMH, the silence of material existence and of restriction to form, and it is the division of the Word which binds it to the material world of Assiah (see Gematria). The sequential nature of the number also implies the progression from Hod to Yesod, from the Creative world to the point of crystallisation, but this may be introducing the artifice of the Graphic representation of the Tree of Life, I am not certain. R:RPSTOVA the synthesis of Macrocosm & Microcosm by the sacrifice of Initiation to Hadit (Atu XV The Devil:Baphomet), Destroys the Fortress of Self exposing the Dominion of the True Will in the Union with the Word ABRAHADABRA, the Magick light extended and, in combination with the previous portion, this extension of the Word is restricted to manifest in Assiah. This is very suggestive of the Binding of the Wiccans or of the manifesting of the LVX in the Golden Dawn Neophyte Ceremony etc. A:L this Word then takes the form of the Hermit, the Holy Guardian Angel And Abrahadabra, His Knowledge and Conversation is attained. Note also that this portion then spells AL, the name of the Book as it was explained to 666. |
By this interpretation, requiring only a rudimentary Qaballah to comprehend, the formula implied here is for the Invocation of the Holy Guardian Angel (at least), and this being in resonance with the known nature of the Word ABRAHADABRA, the English Qaballah still seems to fulfill the requirements which were posited for it at the beginning of this investigation. This Key is in no way in opposition to anything which the Beast knew about the Book, indeed the Qabalistic interpretations used here have come only from the Beasts own Books, and then I have merely quoted his own interpretations of the various values. At the same time, the newly revealed English Gematria already begins to form a cognisant system of symbolisms in its own right, which is relatable to traditional Hebrew Qaballah (this might be said of any system whatever, though, see The New Comment). The constant repetition of the number 72 and of 16 as well as the repetition of certain values in the test formula, as well as the large number of mystic numbers generated by the investigation however, seems to merit further experiment. There are a further number of verses which mention a key, or have some mathematical component, so the logical course is to investigate these serially.
That which I have just outlined above was communicated to me in an instant during my moment of clarity or epiphany. The possession of this Knowledge allowed me to operate the Key immediately, and rashly perhaps, I did as I have explained already. For where there is fear I am not. But Knowledge, as we all Know, is an Illusion, but it can be a carrot on a stick for the donkey Mind, and thereby might this Knowledge become Understanding. This process has taken 17 years, so far. Immediately after finding the Key and elucidating all of this I began to look at some of the other puzzles in this Book, most notably the injunction to paste the sheets from right to left etc., but so far only the Gematria of the Book is clear to me, so I have been given to assume that I have only that part in it.
The immediate consequences of the performance of the ceremonies based upon the formula of Ch II vs 76 were unusual enough to merit mentioning. Almost immediately after completing the three ceremonies my life became filled with people, and with material goods. I hardly spent a moment alone again until late January the following year (1984). Every frivolous whim seemed to be fulfilled to overflowing and my life transformed from one of relative solitude and quiet contemplation, to a constant party overnight, without my ever realising where all of the people had come from. Also the apartment which I shared started to become infested with Beetles. Beetles of all sorts , sizes, colours and shapes were inside or under everything. Australia is The Land of Bugs, but I had never witnessed anything like this before. These beetles were witnessed by scores of people and no one else was being over run by them, and it became apparent that it was a localised event. Several people collected these beetles in match boxes as keepsakes because it was so unusual.
I knew from all of this that I had made a significant step forward on the Path, and I assumed that I had stumbled upon what everyone else already knew about the Book. My lack of reference material in relation to Thelema and because I had not found anyone outside of my immediate circle who was interested led me to believe that Charles Stanfield Jones had already found all of this, and that one day I would find a book which explained the whole thing as clearly as I had seen it. It wasnt until 1997 that I even knew that Frater Achads key hadnt revealed values for the entire Alphabet, and it began to dawn on me that this key had not been seen before.
As a consequence to the above, although I was not isolated (I actually went to live closer to my Witch friend, and even though I am not religious, I participated in some pagan festivals and so forth over the intervening years), so I have had contact with other spiritually mind individuals, but no other had taken up the Art of Gematria or the Holy Qaballah, and so I was truly alone in my way along the Path. After the dust had settled from the events of September 5th 1983, I began to have the time to take stock of what had occurred and I knew that I was only just begun to tread the Path and that the next obvious objective was to use the key that I had found to invoke the Knowledge and Conversation of my Holy Guardian Angel. To facilitate this Opus, I determined to continue to study the Book of the Law by the Gematria that I had found and so I set about investigating the verses outlined already in the text, as well as spending the effort to improve my Hebrew Qaballah and to perfect myself in Magick by the methods outlined by the Beast in His various Libri.
This investigation into the key verses yielded the following results:-
The first verse to specifically mention a key is Ch I Pg 3 vs 20 (sic); The key of the rituals is in the Secret Word which I have given unto him.. Examination of the salient points of this verse by the methods outlined above renders the results:- Key = 54, meaning a definite article, implement, or artifice, for unlocking something, in this case the rituals. 54=2x(3 cubed) indicating a material extension of Binah. Also, the key=42+54=96 the enumeration of AL ADNI Lord God, but also a significant Name in relation to Qelhma. 96 also possesses many mathematical qualities such as 3x (2 to the fifth power) incorporating the first three multiple primes etc., all of which points at the mathematical nature of the key. Likewise, rituals=104, or 52x2 Nuit extended, and so on, but it is also the enumeration of Tzaddai spelt in full. Rituals, from the Latin ritus, implies the manner of performing Divine Service, or a Book containing it (I am surprised that the Beast never made this connection himself). The addition of the to the equation produces the sum 42+104=146, the number of Soph, the limit (see 777 & Gematria), thus the rituals are Nuits Divine service, and the key of their performance is in the understanding of the Word, and in the identification with God as the Holy Guardian Angel. This is supported by the next portion of the verse, the Word being Secret, but Nuit has given it to the Beast already at the time of writing. Thus Crowley knew that Abrahadabra was the key to the Book of the Law, as well as the Great Work, thereby connecting the two certainly. Secret is=90, Tzaddai again, this time in a more material extension because of the connection with Atu IV The Emperor. Word has the sum of 67, the number of Binah, understanding, and I think that the correlation is clear, Understanding comes by the Word. 90+67=157, the enumeration of TzDQH a giving freely (see Sepher Sepheroth), but this may stretch the point a bit far. Given=63, from the old Norse Gyfu a Gift, implies by the choice of word to imply a rune, or a mystery. Unto=52=Nuit, implying that the receiver was the Beast and that the giver was the Goddess. Him=40, Mem Atu XII the Hanged Man, so the gift was of the initiation to Nuit, although he knew nothing of it because it was secret. The work of returning the Word Abrahadabra to its true place was the initiation into its myriad mysteries for the Beast. Note also that 63+42+40=155, ADNI MLK, the Lord of the Earth, which was the Beasts reward for his Divine service, 1+5+5=11 also a thought provoking attribute of this stanza.
The first verse in the Book of the Law which has a defined numerical component is in Ch I Pg 5 vs.24-25 (sic). I am Nuit, and my word is six and fifty this is followed by the adjuration; Divide, add, multiply, and understand.. I am = 19, the feminine glyph expressed in masculine (ie Fire, Air & Jupiter) terms. Nuit=52 the enumeration of AIMA the fertilised Supernal Mother, so the Goddess is represented as extended, that is, She expresses Herself via the agency of Hadit. Next my word is 58, ChN:the secret Wisdom and 67, Binah:understanding, Chokmah and Binah, Father & Mother etc. The sum of these two words is 125 which is 5 cubed, Nuits word is the Microcosm extended by itself. Now the number is given, but in words so that a deeper meaning may be drawn from them, six and fifty is 66+26+94=186, the value of Qooph spelt in full. Nuits Word is related to the passage of the Gates of Initiation. 66 is the mystic number of 11 and thereby related to Aleph, and to Abrahadabra. 26 is YHVH, Tetragrammaton (vide supra). 94 is the enumeration of YLDYM:children, already mentioned in the text Ch I Pg 1 vs.5 and significant to the symbolism of the whole Book. Horus is after all a Twin Child God. 94 is also Hadits number 47x2, or the essence of the Path extended (see 777). Thus the Goddess Nuit extends Herself via the masculine agency of Her Word, which encompasses the secret wisdom of the Elements and their extension into the material world, and further, this Word is the Magick Light of Unity extended (ie. As Nuits children? Perhaps this is extrapolating upon the Qaballah just a bit far) through the Gates of Dawn/Initiation.
The next verse, 25 (sic), should support the above postulate if the Key here employed is truly a consistent system, at least in some superficial manner. Divide=43, and is the number of orgasm, especially male orgasm (see 777), which is in itself an expression of the Great Work accomplished. Divide from the Latin divisum- dis:asunder vid:to separate, the male orgasm is essentially the evolved replication of cell division, the means by which the organism reproduces itself. Add=10 which equates with DV meaning two, implying the sum of the simplest mathematical expression, 1+1. 10 is also the mystic number of Chesed, whilst at the same time it suggests the sphere of the Elements. To add is to increase the material forms of Nuits Word.
Multiply=146 which is the number of SVP, Soph limit. Also of AiVLM the World. Multiply is from the Latin words; multus;much and placare;to fold, meaning to increase the number of: to accumulate, to magnify, to reproduce, to become more numerous, to perform the mathematical process of multiplication, which is in truth to repeat the process of addition a specified number of times. Because of that it seems to imply that the expansive interpretation of multiply might be more accurate, rendering the possible interpretation that the verse adjures us to extend ourselves to the boundaries of our Universe. Note also that 146=73x2, Chokmah and Gimel, the two Paths to Kether (see Gematria).
And =26 (vide supra)
Understand=139 the enumeration of HDQL, Hiddekel, the River Eastward in Eden (see the Golden Dawn). This implies that the Understanding flows out of the East or appears as a Dawning of comprehension. 1+3+9=13 so the understanding is of Unity. and understand = 26+139=175 or 7x (5 squared), the Holy 7 extended to the Microcosm. Also 35x5 is AGLA extended by the microcosm, but this is really the same thing.
On the surface then this verse instructs one to divide Nuits Word, which was done firstly into ABRA + HAD + ABRA and then Her Word was further divided into portions in ChII vs 76. After this division, even into letters, then next step is to add, find the sum of the values. Finally this process is repeated until the numbers to be added are exhausted and the sum is arrived at. The divided word of Nuit has had its element values added together, and the process has been repeated until the sum of the whole equation has been elucidated, and by the agency of the formula of Tetragrammaton (and=26) this knowledge of the sum of the word can become understanding. The enumeration of the entire passage is 43+10+146+26+139=364, the number of AVR MVPLA the Lux Occulta and of HShTN or Satan, conveying the impression that this verse is the method by which to become enlightened in the Secret Wisdom of Hadit. Verse 24 supplies the information and verse 25 informs one how to apply the information of how to unite Macrocosm with Microcosm.
The next verse of relevance to this inquiry is Ch I Pg 12 vs 46-48 (sic),
| 46. | Nothing is a secret key of this Law |
| Sixty-One the Jews call it, I call it | |
| Eight, eighty, four hundred & eighteen | |
| 47. | But they have the half: unite by thine art |
| So that all disappear. | |
| 48. | My prophet is a fool with his one one |
| One, are they not the Ox and none | |
| By the Book? |
Nothing is 93 implying that AIWASS is a secret key of this Law, and the English Gematria of this Angels name is 0+0+35+0+29+29=93. Therefore AIWASS is equal to 93 in Hebrew, Greek & English, connecting all three of these Qaballah. This secret key (vide supra both words) is 90+54=144, the square of 12, and a very perfect number expressing the extension of the Zodiac. Law=52 which is the enumeration of AIMA the Supernal Mother, but 52 also equals NUIT. Nuit and Her Law are one thing, and that is Nothing, which is expressed by 93 Aiwass. Sixty-one=136 (the mystic number of Kaph, Jupiter) +21 (the mystic number of Sol) = 157 which is the number of ZQN the lingam (see Sepher Sepheroth), but 1+5+7=13 Achad, and this sums up the idea of the Jews not recognising that AIN is a part of the Trinity. Jews=77 which is 7x11 the Holiest extension of the Magick Light (see Gematria) and call it =37 Yechidah +31 Al = 68 which is 17x4 IAO expressed as the Elements, but also ABVS, an enclosure, corresponding with the essence of the text, to call it something is to enclose it in a meaning. Nuit then encloses it as eight=51, 17x3 and an extension of IAO, the trinity of Isis Apophis Osiris, eighty=90 therefore Atus XVI & XVII are implied by these values, a symbol of Abrahadabra, which forms the trinity of Nuit Hadit and the Candidate for initiation, as implied above, note the sum of the Atus is 33=11x3, the magick light extended in trinity. Four =34, hundred=69 & eighteen=72 (I am assuming that the Beast heard the figure pronounced in this way as he recognised it as the value of Abrahadabra vide supra). 34 is a number of Jupiter, and the enumeration of AL AB, God the Father, 69=23x3, life extended as a trinity, (34+69=103 NBAIM Prophets), & 72 is Abrahadabra etc (vide supra). 34+69+72=175, a Holy number of Venus, implying that the Word Abrahadabra is a formula of Holy Love. 175=35x5 AGLA the eternal Lord of the Earth as microcosm, the goal of ABRAHADABRA. (Note that 51+90+175=316 ShChCh:to worship, to bow down. But this is perhaps a bit obscure).
The next verse reinforces this interpretation, half=35=AGLA (vide supra), the Jews have only the masculine half of the Trinity, Unite=52 by=40 Thine=63 Art=58 all number dealt with already except 63, the number of SG:Briahs secret nature. Union between the Secret Natures of Chokmah (58) the Father and Briah (63) Mother is indicated, and this by initiation to Nuit. So=29 the magick force itself, that=72 Abrahadabra, all=34 AL AB (vide supra), disappear =107, BITzH an Egg (see Ch II Pg 12 vs. 49). 107+34=141 QMA , prima (but this too might be too extreme an interpretation of the facts). Thine art = 63+58=11 squared the magick light extended. 52+40+63+58=203 ABR, the initials of the Jewish Trinity, which are to be united into one masculine Godhead in relation to Nuit and Ra Hoor Khuit of the Thelemite Trinity.
The last part of this passage admonishes the Beast for a fool with his 111, my=58 and prophet=115 or 23x5 Life in microcosmic extension, 58+115=173 GL AiINI, lighten mine eyes (a bit of a long bow to draw here, but it makes reference to Hadit as Baphomet Atu XV). Fool=24, already interpreted (could it mean that the Beast is a fool before the 24 Elders, and therefore invincible with his Word? This stretches the investigation too far, I fear, by introducing the artifice of Religion). 24=AHIH, existence. One, one, one is 63 (vide supra), indicates that at the communication of the Book the Beast too was mistaken about the Trinity, but the Goddess corrects him; are they not instructs that they are of Nuit (Nuit=52=Not), Ox=37, Yechidah, and none=42, the 42-fold name of God (see The Vision and the Voice-Crowley), whilst 3+7=10 & 4+2=6, indicating that this trinity of 111 is of Kether and of Tiphareth, they are the Highest principal of the soul and the Perfected Consciousness, which Nuit now posits as one thing, By the instructions here, an adjustment to our concept of Trinity is made and the means of adjustment is also made clear. Note that Ox combines the ideas of the Path of Resh (Atu XIX)=x and of Aleph, the Word is of the Twin Gods, also the Hebrew letters of these Paths spell AR: light.(this last may be outside the parameters of this inquiry though, so it is only for consideration that it is included). by the Book = 40+42+16=98 the enumeration of Glad Word, but at the very least these numbers are readily cognisable.
Chapter I Page 19 verse 60 (indicating perhaps that this is the synthesis that is the feminine glyph 19), My number is 11, as all their numbers who are of us. The Five Pointed star, with a Circle in the Middle, & the circle is Red. My colour is black to the blind, but the blue & gold are seen of the seeing. Also I have a secret glory for them that love me. This verse in four parts gives my=58 (vide supra) number =68=17x4 IAO expressed as the Elements which has the sum of 58+68=126 = IHVH ADNI AGLA (see Sepher Sepheroth), the three Names invoked in the Pentagram Ritual which correspond to East, South & North, omitting Nuits direction, that of Darkness and of the setting Sun. Thus as all=29 the magick force and 34 17x2 IAO as well as 29+34=63, Briahs secret nature, all refers to the company of Heaven, extensions of the Trinity. Numbers has the value of 97, the number of Amoun, the oldest God, thus the numbers even were conceived of as were the company of Heaven. Who=46 (23x2 Chiah extended) are =27 (3 cubed) of = 7 Netzach & the Holiest of numbers us =29 the magick current, also 46+27=73 Chokmah & 7+29=36 6 squared and a definite solar number, but also the mystic number of Hod. The sum of this phrase is 109 which is AiGVL a circle or a sphere, implying that the Goddess Who is the Circumference.
The next portion of the MS was filled in by the Scarlet Woman after the fact, as it were, and so it must have some significance as it is her only contribution to the penmanship in the Book. Five =38 which is 19x2 the feminine glyph extended, pointed is 80 and thereby Atu XVI the Tower and so Mars/Horus and star =87 , the number of LBNH and therefore a Lunar number also implying Yetzirah. (87=29x3 definitely linking this number with the feminine principal). 38+80+87=205 or 41x5, AM the Mother expressed through the microcosm, or in this case its most perfect symbol. Circle=50 and thus Nun XIII Death, and this circle is the symbol of Hadit as Death, concealed within the star of Nuit. Middle =46 which is 23x2 Chiah extended (vide supra) and the colour Red =32 or 2 to the fifth power, the Word expressed via the pentagram.
The colours of the Goddess are next, my 58 (vide supra) colour=47, the number of the espirit de travail (see 777) but also the enumeration of HADIT in English. Nuits colour are therefore expressions of Herself as Hadit. 58+47=105 the mystic number of Daleth, Atu III the Empress, which in itself may be significant (see Ch II). Black =36, the mystic number of Hod, which implies the analysis of any colour is to compare it against no colour. The Blind=44 which as 4x11 represents the corruption of the Magick Light in the material world as DM blood (see Gematria), those that analyse God by their moribund intelligence will see only Black in Nuits colour. But is the exception =32 2 to the fifth power again, the Word in motion, defining those that are of the seeing. The blue =18 is ChI living, and 42+18=60 which is Samekh Atu XIV Art implying a living synthesis in this, the living colour of the Goddess. & gold =31 which is AL of course, being the complimentary colour to the midnight blue of Nuit (as for the flashing colours of the Golden Dawn Flashing Tablets). 60+31=91 which is AMN: Amen and the mystic number of Gimel, representing thereby a veil of Kether. Seen =50 Nun and Atu XIII Death of =7 the =42 seeing =59 (the yearning of the yoni for the lingam see 777) and 50+7+42+59=158 which is 79x2 or IAChIN + BaiZ jacin & Boaz the sum of the names of the Pillars of the Temple of Solomon, the seeing are looking through this mystic portal.
Finally, the Goddess offers a secret =90 glory =92 (PChD or Terror an alternate title of Geburah) which is 23x4, or Chiah, life extended in the Elements, whilst 90+92=182 the enumeration of Melekh HaAlhim, the King of the Gods and it is of course 91x2 or AMN, Amen extended. Love =50 and implies that the Love is of the devotion of Her Initiation and me =19 the feminine glyph, the sum of these two being 69 Chiah extended as a Trinity (ie Light, Love & Liberty etc).
Chapter II has two more verses with an unexplained numerical component Page 3 verses 15&16
15 For I am perfect, being not, and my number is nine by the fools, but with the just I am Eight, and one in eight: Which is vital, for I am none in deed. The Empress and the King are not of me: for there is a further secret 16 I am the Empress & the Hierophant. Thus eleven as by bride is eleven.
Perfect = 91 Amen and the mystic number of Gimel, Hadit is the oldest God. Being = 31 AL and Not =52 = Nuit and their sum is 83, the number of consecration, Hadit is motion rather than matter, the consecration rather than the God of the working. My Number vide supra, these qualities are the same as Nuits because She can only ever express Herself as Hadit. Nine = 42 AMA the unfertilised Mother, by the fools =24 (vide supra), those who mistake the Trinity as of masculine unities in Triune formation. The exception, but=32, are those that perceive the Word as the microcosm, and they are Just =73 Chokmah or Gimel, the two paths to Kether, so this is the path of the Wise, that count Hadit as eight =51=17x3, or Hadit as the entire Trinity of IAO as well as one =21, the mystic number of Sol, in =21 again and eight =51, which is that He is also its integral elements, and the sum of 21+21+51=93=AIWASS, and thereby Hadit is the Minister of Hoor, and by inference, Hoor himself (as our little self see the New Comment), and thus Hadit shows Himself to be AB BN RVACh, Father Son and Holy Spirit. This is vital, ie of life (from Latin: vita, Life), and vital = 81= 9 squared and suggests Luna, or Yetzirah extended. It is also the enumeration of ALIM, Gods (although see Magick in Theory and Practice for an explanation of this formula as one of witchcraft). Hadit is stating that the above information is about Life, only one of His personas, and that He is none in deed (the word indeed seems broken in the MS) which renders the sum 21+(21+10)=21+31, the mystic number of Sol and the Name AL and the sum of these is 21+31=52, the number of Nuit, so Hadit expresses Himself as an extension of Nuit, thereby complimenting Her.
Next there is another obvious Tarot correspondence in the text, the Empress = 42+127, (a material number) the two implying the material 42-fold name of God, and 42+127=169=13 squared, and thereby a number expressing Unity extending itself. And = 26 IHVH, and the King is 42+45 which is the mystic number of Yesod, and thereby of Luna and of Yetzirah. 42+45=87 which is LBNH, Whiteness, and a name of Luna also. 169+26+87=282 RVCh CIIM the spirit of Lives, also 191 AINPIN the countenance x 2. These concepts are not 27+52=79 implying the Pillars of the Temple of me=7+19 (Venus and the feminine)=26 IHVH and 27+52+7+19=105 which is the mystic number of Daleth as well as 21 (the mystic number of Sol) x3. Thus the spirit of lives and the countenances of the Gods and Goddesses of the material world are the Gateway to invoking the Love of Hadit. The Gods of men form the Not of Hadit, as I am alone, there is no God where I am. But the Empress, the material Gods of men, their devotions, and the Hierophant =42+124 (31x4, AL extended in the Elements as IHVH)=166, ChIIB MMVN the defendant or petitioner as well as 83x2, extended as consecration, agreeing with the number 124 anyway. 169+166=335 which is 3+3+5=11 as indicated in the text, but also the mathematics is 67x5, the Understanding expressed as a microcosm. (also Melekh Melaki HaMelikim, the King above the King of Kings, but this may be too obscure). In any event, Hadit is defined as devotions and as the devotee, consecrated to Nuit by the magick Light 11, and thereby as an enlightened microcosm. Thus =71 as does eleven =71 which is the number of silence and restriction, but twice 71 is 142, QMA prima, first indicating that Hadit is the first or essential emanation from Not. My Bride =58+33 (3x11 and the magick light as a trinity, but also the number of lies and of Saturn) has the sum of 91 Amen, Both Hadit and Nuit are equally as old and archetypal as each other, thereby further complimenting each other. Is eleven =29+71=100 the value of Qooph and thereby Atu XVIII The Moon, the passage of initiation, but also Kaph, the Palm of the Hand and finally 158 is the Pillars of Solomon (vide supra). Together Hadit and Nuit are a perfectly complimentary pair, and their union can be expressed in any symbol which has this complimentary nature, thus the correspondence with the Pillars, verifying their efficaciousness in the new Aeon.
Continuing with the inquiry, the next verse to relate to the key, which remains unexplained, is Ch III Pg 1 vs. 1 Abrahadabra! The reward of Ra hoor Khut. Abrahadabra=72 (vide supra) and the reward =94 Children, as well as 47x2 the extension of the essence of the Path (an apt description of Hadit in light of the above). 42+94=136 the mystic number of Kaph, Atu X Fortune, the reward is True Will. (the reward of = 143=11x13, unity extended as the Magick light in an elevenfold Word). Ra hoor Khut is 27+38+57=122. Ra is Sol and the value 27 is Saturnian, the Atu XIV Art implies a synthetic nature, Hoor is Harpocrates and Khuit/Khut is a name of Khem & of Amoun (see the old Comment) Hoor =38=19x2 the extension of the feminine principal. 57=19x3, indicating that the same feminine principal is a trinity. The total enumeration of 122=61x2 the Not extended, again resonant with the concepts of the Book (see the New Comment). 122 is also GLGVLIM the cycles of animal life.
Ch III Pg 5 vs.19 has already been revealed by the Beast to be answered by CYHAH + 666 which gives the enumeration of 718. Note that this word is 52 which is the number of Nuit, so the Number of Nuit + the number of the Beast = 718. The Stele shows this exact thing, with the graphic aspect of the composition being a picture of Ankh af na Khonsu worshipping Ra Hoor Khuit whilst Nuit is as the vault of Heaven, and the text of the stele also implies that the Goddess will kiss the Beast as the secret ardours of Hadit. Stele = 77 which is the number of OZ and thereby of Baphomet the idol god of the Templars, but also as 7x11 the Holiest extension of the Magick Light. The Abomination of Desolation is 42+93+7+103, the Mother AMA, as yet unfertilised, AIWASS, Devotion, and NABIM , Prophets, a talisman of the prophets of Aiwass and of Not. The sum of this phrase is 245=5x(7 squared) perfection extended into the microcosm. Count well its name is 55+69+60+40, the mystic number of Malkuth , and 69=23x3 Chiah extended as Trinity the sum of the adjuration to count well is 124, the Hierophant, but also 31x4 AL/Law extended as the Elements. Its name is 100 Qooph and the Atu XVIII the Moon, indicating the gates of the Dawn of the Light . the sum of these is 224 DRK : the Path which is also 56x4 (see Ch I), and so it is a Pantacle of Nuit. 718 might be seven one eight, in which case it is 83+21+51=155, the consecration to Sol by the Trinity of IAO and 155 is Adonai Melekh, the Lord of the Earth. It names this as the Pantacle of the Prophets of Nuit, and they are as the Lord of the Earth, that is they have attained the Knowledge & Conversation of their Holy Guardian Angel. As Seven hundred & eighteen it is 83+69+72=176 leOlahm, to eternity, another name of the Goddess.
The last verses to have a numerical riddle, or a mystery hidden in them seem to be the last three verses Ch III Pg 21 vs. 73-75. 73 Paste the sheets from right to left and from top to bottom: then behold! 74 There is a splendour in my name hidden and glorious, as the Sun of midnight is ever the son. 75 the ending of the words is The Word Abrahadabra. The Book of the Law is Written and Concealed. Aum. Ha.
I have followed out the first portion, pasting the sheets in various patterns, to little avail. Paste, comes from the Greek : pastos: to sprinkle, salt and is related to pastry, glue first being made with the same materials. Sheets is from the O.E. sceate: corner and implies the four cornered nature of the pages themselves. The directions given are as the Qaballistic Cross, implying that the actual pages of the Book, if sprinkled, would reveal something to behold. Paste =88 or 8x11, an ultimate extension of the 2, and sheets =100 Qooph, a magickal manipulation of the material of the Book itself, the entire phrase =240 24x10 and the enumeration of Myrrh, the perfume sacred to Binah. Right = 87 the number of Lebanah, implying Luna and Yetzirah, whilst left =55 the mystic number of Malkuth, the Kingdom. The entire phrase = 216=16 squared, the connotation is that this action is of Hadit extended. The phrase from top to bottom is made up of similarly familiar numbers and has the total enumeration of 220, the number of verses in the Book of the Law, a fact as yet undetermined at the time of its writing, although I am certain that the Beast worked it out consciously later on as: 65 pages+1 Title Page =66 Pages, which is 220x.3333333etc. Then behold = 97 = Amoun, and BN ADM, the Son of Man. It is as if this verse is the instruction to a ceremony performed with the Book of the Law as its First Matter, which will reveal something of Ra Hoor Khuit, but I have not as yet fathomed this entirely.
The next verse though is straightforward enough, splendour = 122 (1+2+2=5) = Ra Hoor Khuit, my name = 98 = Glad Word etc (vide supra), hidden = 42 the Mother and = 26, glorious = 82 a fertile number of Luna. Hidden + glorious = 42+82=124=31x4. 42+26+82=150 AINK: thine eye, thus in the name of Ra Hoor Khuit is hidden, as the Glad Word of Not, is the elemental extension of AL, God, and this is as Horus eye, suggesting Ayin the eye or the secret force of Ra Hoor Khuit is the Silent God Harpocrates, Whose Name is the centre of His Compliments Name also. This connects Ra Hoor Khuit & Hoor parr Kraat as complimentary concepts of the same God, Horus, Heru Ra Ha (see Ch III vs 35).
As the Sun of midnight, who is of course Khephra, the Beetle Who carries the Solar Disk through the underworld and a symbol of Atu XVIII the Moon. This phrase = 29+42+50+7+96=224=61x4, implying that the Sun of midnight is Not manifested as Night. Note that Sun=50 the number of Atu XIII Death, initiation, and midnight =96, a very perfect number related as 24 is to the Dyad as the Circumference and the centre. This phrase suggests then that initiation to Nuits ordeals is ever the son which adds as 60+42+50=152= BNIMN benjamin, the son of IMN=100 Malkuth, ie the Son of Man, as well as being a number of mitigating one thing for another (see Sepher Sepheroth for the correspondence). The son =92 or 23x4, Life extended Elementally. The man who initiates will always be the Son of Man.
Ending = 66 the mystic number of Aleph, and 6x11 consciousness of the Magick Light, words = 96 AL ADNI the Lord God is the essence of the words. The Word = 42+67 (Binah; Understanding), =109 the number denoting a circle or sphere. Implying that the Book of the Law is the Understanding of the Lord God by the Word Abrahadabra. The Book of the Law has the enumeration of 159 53x3, Lover as a trinity, or the Book of Love in three parts. The Book is 42+16=58 the secret Wisdom, and the Law = 47x2 and children (vide supra). The correspondences are too numerous to include.
Written implies that the physical action of the Beast writing was an effort which can now cease, for the moment, and concealed hints at there being an as yet unknown element to the Book ( which there obviously was). Written = 145, the value of the Paths of the Lesser Countenance and 29x5 the magick current expressed as microcosm. Concealed = 49 the perfect square of 7. 145+26 (and) +49=220 the number of verses in the Book of the Law. Aum =19 the feminine number of Nuit throughout this investigation, and Ha = 11 the number of Magick and of Abrahadabra (the ending of the words is The Word Abrahadabra, vide supra). The entire stanza is 159+29+220=458 the enumeration of ChTN a covenant, as in the Ten Commandments.
The only remaining passage of the Book which fit the parameters of this inquiry is Ch I Pgs. 16-17 vs 54-56 (sic). This is the portion of the text which identifies the child who shall expound the mysteries concealed in the Book & in the MS itself, which Nuit has forbidden interference with;
Change not as much as the style of the letter; for behold thou o prophet shalt not behold all these mysteries hidden therein. The child of thy Bowels he shall behold them. Expect him not from the East nor from.(page break in MS)the West, for from no expected house cometh that child. Aum! All words are sacred and all prophets true; save only that they understand a little, solve the first half of the equation, leave the second unattacked. But thou hast all in the clear light, and some though no all in the dark.
Change =44 DM Blood, and the corruption of the Magick Light in the material world (see Gematria), and not =52 already familiar, while style = 116=29x4, the magickal current extended by theElements, and letter, which certainly must be significant, =106, the enumeration of Nvu, a fish and the letter of Atu XIII Death, but the enumeration of the entire stanza is 458, a covenant, so the covenent is in the handwritten MS. This is elaborated on by the Beast being informed that; behold=34 AL AB + thou 42=73, Chokmah, ie here is wisdom for the Beast, o prophet =115 23x5 Chiah expressed as a microcosm, that is the man aware of himself as Hadit, the Beast is thus enlightened but he is obliged to not behold all 34+34=68, ChKM, to be Wise, that he willnot see the other half of his work, without the He that is the mystery of Nuits Name. The mysteries =174=29x3x2, the magick light extended as a Word of the Divine Trinity. Mysteries (from the Latin mysterium: servant) implies that there are many and that these each have their servants. 174= NGVH LV SBIB; splendour that would travel in circles (see Sepher Seperoth), and hidden therein = 132= QBL to receive, the QABALLAH.
The Child of thy Bowels, is the finder of this key, Child =36 which is the mystic number of Hod, and six squared and thereby a very perfect number, as all children are before they are polluted by their environment. Thy Bowels = 81+82, nine squared and 41x2, the Mother extended as the formative world = 163 NVQBH, woman or wife, whereas of thy Bowels = 170 = MQL The Wand (Davids Staff- see Sepher Sepheroth).
This child, he=11, shall behold them=74+34+61, 74 is LMD the Ox Goad, 34 is AL AB, and 61 is Not implying that the magick light of the Ox Goad of AL AB and Not will be beheld by him. The sum of this phrase then is 11+74+34+61=180, an extension of 18 (itself a significant number in the text), which is the number of ChI, Life, and further this number relates to 3 & 2 factorially.
The next stanza tells us where not to expect him from, implying some hidden intention in the text. Expect him not=94+30+52=176 the number of leOlahm, to eternity (vide supra), 94 is ILDIM, children, but also 47x2 (vide supra), 30 is Lamed and Atu VIII Adjustment, suspension of action pending a decision (see the Book of Thoth, Crowley), 52 is not. This tells us that we must wait the arrival of the child, he is not yet, and he is one of many. from the East=53+42+60=155 the number of Adonai Melekh, Lord the King, a name of the Holy Guardian Angel. 53=MAHBH, lover 42=AMA, &60 is Samekh, Atu XIV Art, synthesis, ie not from the Divine synthesis of lovers. Nor from the West=48+53+42+95=138 (23x6) BN ALHIM, the Son of Gods, as well as 48 which is a beautifully symmetrical number with the factors of 3 & 2, and which is the value of Gedulah: Mercy. 53 is lover, 42 is AMA the Mother, unfertilised, and 95 is 19x5, the feminine principal extended in microcosm. So this child will not come from some magickal extension of the Goddess elsewhere and elsewhen, For from no expected house cometh that child. This is (53+21+99+40)+(64+73+36)+19, Aum!. Expected =99 9x11, the magick light manifest as the formative world, 40 is Mem, the Mother as the Element of Water, and the sacrifice of Initiation. The sum of the first phrase is 213 which is ZVR, a stranger (see Sepher Sepheroth). Cometh = 64 which is the ultimate conscious extension of the 2, the Word, that is 73 Chokmah, and Child is 36 (vide supra). The sum of these is 173, GL AiINI, lighten mine eyes, the entire stanza has the value of 213+173=386+19(Aum!)=405=3x3x5, the ultimate extension of the Trinity as microcosm. This child then, cannot be made or invoked in any way, for he is fated to follow the beast.
Next it commands that all words are sacred, 34+96+27+64=221=17x13, they express the Unity of the Trinity IAO. And then it continues and all prophets true=26+34+144+58=262, 131 SMAL, and thereby Hadit x2, 221+262=483 NVShA AiIN, the eye of iniquity. Save=62 BNI, sons, and 31x2; only =75=3x5x5 and NVIT in Hebrew, that =73 they =81 Understand =139, HDQL, the river to the Eastward in Eden (see the Golden Dawn) , a little=95 or 19x5, 62+75+73+81+139+95=525, ALHIM TzBAVTh, the Lord of Hosts, the Divine Name of Netzach. These prophets are the children of Nuit as microcosms , save only=137 QBLH, and AVPN the Qaballah and a Wheel, whilst they Understand = 220 the verses of the Book, these prophets are of the Wheel of the Book of the Law, and their message is a Qaballah, of Nuits extensions into microcosm.
Now the Goddess adjures the Beast to Solve the first Half of the Equation, being 79 (implying the Pillars)+42+74 (the Ox Goad)+35 (AGLA)+of the 49+77 (7x11)=355, 71x5 Binah as silent understanding extended in microcosm, attain to understanding. And to leave the second unattacked=50 (Mem)+42+58(secret wisdom, ChN)+85(Peh spelt in full)=47x5, and Tzediqial, the Archangel of Chesed. Come to a silent understanding of the task, the Great Work, and allow Hadit to formulate the rest.
The Beast, however, has all in the clear light But 32+ Thou 42+ hast 71+ all 34+in 21+ the 42+ clear 47+ light 68 (17x4)=357 NVShA Iniquity, one of the eyes referred to above, and some though not all in the dark, 26+48+62+52+34+21+42+47=332 AVR HIQVD, that which makes the light strong. Also suggestive, 26+48=74 the Ox Goad, 62+52+34=MAZNIM, Libra the scales 42+47=99 9x11 the magick light just short of manifestation+21=120, the mystic number of He and the enumeration of the Name ON (see Gematria). The Beast is the inspired prophet of Nuit but he does not see that which makes the light strong, ie the key to the values (Latin, valare to be strong), and this is so.
So it is that this key is to the order & value of the English Alphabet, and the symbols to attribute them unto. It has been defined by the line and by the circle squared, it has elucidated Abrahadabras inner properties, and it successfully interpreted Ch II vs 76, as the Beast himself said the key must, as a Cabalistic test on the ordinary pattern. Every passage of the MS which delineates the key is found to be in resonance by it, with traditional Holy Qaballah, and these correspondences are the simplest (I hope) available, based as they are, upon basic mathematics, and the direct interpretation of the Sepher Sepheroth, Gematria & et al. The large number of mystic numbers etc. which are generated by these values of the letters, implies the same sort of symmetry apparent in Hebrew between letters and numbers.
Finally, I myself, seem to fulfill the requirements of the identity of The Child of Thy Bowels by the enumeration of my name. This fact, known by myself since 1983, has never especially pleased me. I considered my involvement in this as an invasion of my life, and to some extent I still do. Because of this I set out to prove the key and perhaps Qelhma to be nonsense, and failed. The deeper one looks the deeper that this key will go. I have neglected the Yetzirac attributions in most of these passages, but they are equally as informative, rest assured.
Having failed to disprove this key, I decided to ignore it. I abandon the study of Gematria altogether for eight years. In that time I did very little magick. I concentrated upon my material responsibilities and my material life, but all along I Knew the Truth, the Book would not go away. In 1994 I began to re-examine the key, and by its power & Truth I have scaled the Paths of the Serpent and attained the Sacred Magick, the Magnum Opus, and always it has proven itself by its SUCCESS.
Success is thy only proof
Success = 93 = AIWASS, is thy = 29+81=110=11x10, only =77=7x11 and proof =57, by Aiwass is the Holy magick light extended to the Kingdom as the Word of the Trinity.
They shall worship thy name, foursquare, mystic, wonderful, the number of the man; the name of thy house 418
They Shall = 81+74=155 Adonai Melekh, Lord of the Earth; worship =125, five cubed, the microcosm extended to the Trinity, thy name =81+40=121=11 squared. They shall worship =280, the number of squares upon the walls of the vault (see Golden Dawn Adeptus Ceremony) and the sum of the whole is 280+121=401= Ath, Alpha & Tau, Essence, Alpha & Omega. Foursquare =99=9x11 , SISHIVN the clay of Death, also 3x3x11. Mystic =121, and wonderful =112, 66x2, 12x11, Nuits magick Light. The number of the man =201 AR Light, the number=110=10x11, of the man=91, Amen, expressing the Beast as the material aspect of Nuits Word, which is a prayer, Amen. And =26= IHVH, the name of thy house =(42+40+7)=89, GVP the body, +(81+40)=121, eleven squared =210, the mystic number of Yod, Atu IX the Hermit, and also, the Beast is the body of Adonai, and the Minister of Hoor paar Kraat. 418 = 13 Achad. Four one eight =34+21+51=106= Nun the Atu, XIII Death, of initiation. Note that thy name, mystic & thy house all equal eleven squared, as if the name, the essence and the physical forms of the Beast are extensions of Abrahadabra, making him the True Prophet and Representative of the Eternal Gods Upon The Earth.
11.And I beheld another beast coming up out of the earth and he had two horns like a lamb, and he spake as a dragon. 12.And he exerciseth all the power of the first beast before him, and causeth the earth and them which dwell therein to worship the first beast, whose deadly wound was healed.. 13. And he doeth great wonders, so that he maketh fire come down from heaven on the earth in the sight of men. 14. And deceiveth them that dwell on the earth by the means of those miracles which he had power to do in the sight of the beast; saying to them that dwell on the earth, that they should make an image to the beast, which had a wound by a sword, and did live. 15. And he had power to give life unto the image of the beast, that the image of the beast should both speak, and cause that as many as would not worship the image of the beast should be killed. 16. And he causeth all, both small and great, rich and poor, free and bond, to receive the mark in their right hand, or in their foreheads: 17. And that no man might buy or sell, save that he had the mark, or the name of the beast, or the number of his name. 18. Here is wisdom. Let him that hath understanding count the number of the beast: for it is the number of a man; and his number is six hundred threescore and six.Rev13 vs11-18
This page last updated: 03/01/2018
